Lifting King Bob-omb

Published 2017-06-20

Here's an age old riddle you've never thought to ask: How many people does it take to lift King Bob-Omb from Super Mario 64?

As a self-exercise in making sure I don't completely forget everything from my Physics course (and also after watching basically everything by Pannenkoek) I wanted to see just how absurd the land of Mario 64 is... and more importantly, how absurd it isn't. No idea if I'll make this a series, but there is a lot of potential in the idea. For now, let's set the following restrictions:

• We have an infinite army of people at our disposal.
• These people average out to the statistical average for the US population, but individually can vary in gender, strength, height, etc.
• People enter a world with nothing but the clothes on their back.
• When any one person gets a star, the world is reset and all people are removed.
• Death by heat stroke or toxic gasses won't be counted, mostly due to Lethal Lava Land and the Bowser stages.
• Goombas are squishy but still bite, fish have bones, bob-ombs are made of steel and explosives, etc.
• If needed, you can break tree branches, scavenge enemy remains, dig holes, scale mountains, carry powerups, etc.
• Generally speaking, assume that everything looks and acts like it would if it existed in the real world, with physics and all. Powerups included.

If you've ever played Super Mario 64, you know that in the very first mission given to you the objective is to go to Bob-omb Battlefield, scale the mountain, and throw King Bob-Omb on the ground 3 times. Scaling the mountain would be easy enough, assuming you can make the jump on the path spiraling around. (And if you can't, just break off some tree branches and make a bridge.) But lifting King Bob-omb? Well...

Slight problem. He's big. Mario (according to some life-size statue that exists) is around 1.55m tall. (Going metric here. You'll see why soon...)

Doing a quick and dirty scale comparison, the ball part of King Bob-Omb is almost exactly 1.5x the height of Mario, or 2.325 meters tall. Pretty big. Also pretty heavy, probably. How heavy? First, what's in a Bob-omb anyways? Nitroglycerin, probably, because that's what's used in dynamite. A Bob-omb is pretty much just a walking stick of spherical dynamite. Let's foolishly assume that we have a 5cm steel shell covering a 222cm diameter sphere of pure nitroglycerin. (Lets also foolishly assume that the nitroglycerin WON'T explode on contact and nuke the entire landscape, even though that's what nitroglycerin kind of does.) How much would that weigh?

Let's start with the inside sphere. It has a total volume of 1.33π * (1.11 m)3 m3, or 5.729m^3. The density of nitroglycerin is 1.6 g/cm^3, or 1600kg/m^3. Multiply your volume by your density and you get your mass, which is a good 9,166.4 kg.

We probably don't even need to at this point, but let's calculate the weight of the outer shell. The volume of a shell is 1.33π(R3-r3), where 'R' is the outer radius and 'r' is the inner radius. For our shell, the volume is 0.813 m^3. The density of steel is somewhere in the ballpark of 7.5 g/cm3, or 7500 kg/m^3. This gives you a mass of 6098.3 kg, which is quite significant. (We are, of course, assuming that a mere 5 cm of steel shell can even hold over 9000 kilograms of anything, but even if it doesn't we could just change the power level thickness of the shell and recalculate.)

King Bob-omb, therefore, has a mass of 15326 kg! For reference, the average car is only 2,300 kg. And now you know why Mario struggles to carry around King Bob-omb.

So, how much force does it take to lift King Bob-omb? Better question: how much gravitational acceleration is there in Mario 64? According to a video by Pannenkoek (the 0.5x A press guy), Mario is 144 "units" tall and has a gravitational acceleration of 4 units every 1/30 of a second. Translated, that's a conversion factor of 92.9 units per meter. If Mario accelerates at 120 units/second^2, gravitational acceleration in the Mushroom Kingdom is 33.45 m/s2 or, more helpfully, 33.45 N/kg. (Any physicist reading will now scoff at me because gravitational acceleration and gravitation field strength are two entirely different concepts with two entirely different physical units that happen to be equal by sheer coincidence, but then proceed to tell me that it's perfectly okay and everybody does it. Physics is like that.) Consequently, this means it takes over 512,667 newtons of force to lift King Bob-omb. Wolfram Alpha tells me that the force of a T-rex bite is a ninth of that, if that helps you visualize it at all. (Probably not, though.)

Back to the original question. How many people do we need to lift king Bob-omb? This one's actually rather easy to calculate with some simple division. All we need is the amount of Newtons one person can lift. (We need to go this roundabout way because of the whole 33.45 N/kg thing going on, which screws with everything.)

Thankfully, some stats by Dr. Lon Kilgore, PhD are here to help. Remember, these are average people, not weightlifters. An average weight is 195.5 lbs for an American male and according to the CDC. and 166.2 lbs for an American female. According to Dr. Lon Kilgore, an untrained 198 lb male can deadlift 155 lbs (70 kg), and an untrained 165 lb female can lift 90 lbs (41 kg). Assuming an average 50/50 split between men and women, we'll get an average of [(70 kg * 9.81 N/kg) + (40 kg * 9.81 N/kg)] / 2 = 540 newtons per person.

Super pedantic note: King Bob-omb's challenge is, and I quote, "Can you pick me up from the back and hurl me to this royal turf? I think that you cannot!" We'll be picking him up from the back... and from the front, the side, the bottom, and basically any surface we CAN pick him up from. It technically fills those conditions, so we should be okay.

512,667 newtons / 540 newtons/person is equal to 950 people. That's quite a large number... especially when considering that the average human (calculated from the average of the two waist circumferences from that earlier CDC link and foolishly assuming that people are shaped liked circles) has a cross-sectional area of 0.0765 m2. King Bob-omb has a cross-sectional area of 4.246 m^2. Even if we assume humans are made of liquid and we can squeeze them into whatever shape works, we can only fit 55.5 people under King Bob-omb. That's a whole order of magnitude less than what we need!

Is there any other way we can lift the King? Maybe, if we cheat a little bit.

Idea: let's build a ramp, and then drop the King off. We're going to assume the the King is stationary, because I don't even want to get into having to deal with him walking around while we do this. We're also only going to go up one meter, because that's probably enough to count.

For a ramp to work, we need to be able to push the King up the ramp. Question: can we push him at all? After all, he is pretty heavy. And heavy things need to worry about friction. Now we need to talk about how friction works. (Strap in, this is actual physics!)

There's two types of friction: static friction and kinetic friction. (There's also rolling friction, but that's pretty much exclusive to rubber tires because of how much they deform.) Static friction is in effect resisting motion until the object in question starts moving. After that kinetic friction is all that matters. And kinetic friction is almost always less then static friction, so what we need to find out is how many people we need to overcome static friction.

We start by looking up the coefficient of static friction of steel on dirt. (We would need to roll him onto the ramp in the first place.) This is surprisingly hard to find, but after a little bit of searching I found an article from the journal Soils and Foundations by Y Tsubakihara, H Kishida, and T Nishiyama titled Friction between cohesive soils and steel. Assuming an "S-0" soil composition (it's not sand) and maximum steel roughness (because who polishes a bomb?) the static coefficient of friction (or "maximum") is 0.59 and the kinetic (or "residual") is 0.53. These seem like the best numbers we're going to get, so let's roll with them.

Let's forget even the ramp for now. Flat surface. Is this even feasible? To compute the force needed to overcome static friction, we use the equation Ff ≤ µFn, where Ff is the force of friction, µ is the coefficient and Fn is the normal force. The normal force is the force along the normal, the force along the direction perpendicular to the surface. The normal force in this case is just the force needed to lift King Bob-omb, our 512,667 newtons. (Think of the ground as doing the lifting here.) Our coefficient of friction is 0.59. Therefore, to get started moving we need to push with 302,474 newtons of force. ...Is that doable?

Let's turn to NASA for statistics to help us. The mean force of pushing from an upright position seems to be 1285 N assuming ideal conditions. Doing the division, we need 237 people. Better, but it is still impossible to have 237 people huddled around one side of King Bob-omb, so we can throw out that plan entirely. (Darn.)

What if King Bob-omb were to start on the ramp? After all, he CAN walk. The coefficient of friction is between 0.2 and 0.5, so let's say 0.25. We'd only need 60 people to move him across a flat surface. Getting better. ...but my sense of scale is falling apart from all these numbers flying around. Let's actually needing to calculate exactly how many people can fit.

According to architect Ernest Irving Freese, the average person is 1' 6" wide, or 0.46 m. King Bob-omb is 2.325 meters wide. We can fit about 4 people. Maybe 8, if some of them kneel and push. But not 60. (And that's not even taking to account that the outer people would be pushing at a strange angle, reducing the force they provide.)

Other ideas? We don't have anything to hang a pulley from. We can't shove him onto a lever, because we can't move him at all. ...not with our muscles, anyways. There is one last thing we can try though: rope.

Who said we needed to PUSH him up the ramp? Let's just create some rope (don't ask me where from. It's rope. Steal it from the railings in the castle or fashion it out of clothing or something), lasso it around King Bob-omb, and get 237 people to just pull. (We're also assuming that the King isn't resisting, because that just turns into a game of Tug of War. And even if he is, we just add more people.) That is a solution that will work perfectly fine.

Now we need to talk about the ramp, something I've been delicately dancing around. I've already stated that it will be 1 meter tall and made of wood. But I've never discussed how long it is.

You'd think that the answer to that would just be "the length of the mountaintop minus a meter or two". But here's the question: where would you get that much wood from? Remember, we have infinite people, not infinite resources. We have to scavenge from the world around us. (Yeah, I know I totally just handwaved the rope into existence, but I hope you are all okay with that.)

The most obvious long piece of wood we have access to is the teeter-totter near the beginning of the level that Mario has to cross. We can easily shove some stuff under that to make it a ramp (because there is PLENTY of stuff to go around). How long is that piece of wood? Using the power of reverse engineering, we can find out.

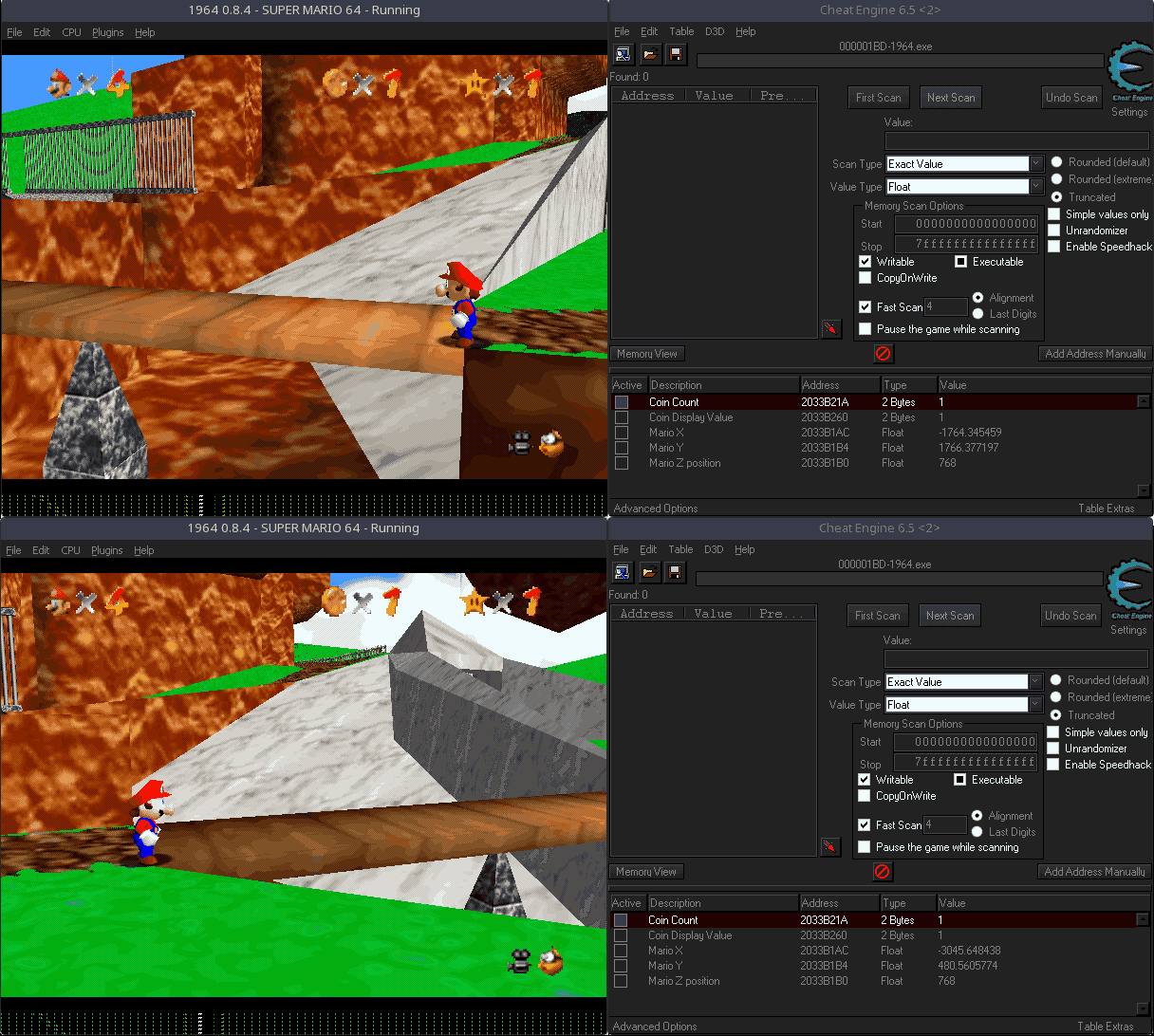
As it turns out I could not find a single emulator that let me view memory. Or even enter in Gameshark codes. I feel like this definitely shouldn't be the case, but after several hours of dragging out old laptops and installing everything and anything, I gave up. So instead, I reached for my trusty old companion: the Cheat Engine. I used it to search through the Nintendo 64 emulator's memory to find Mario's X/Y/Z coordinates, which surprisingly enough worked.

For those of you who are curious as to how I did that, here's the process. First thing I did was search for the number of coins, just to make sure that I could use the Cheat Engine at all. That worked. After that, I had Mario jump up and down and run up slopes while scanning memory to find the Z coordinate address. I had about 8 options, so I used the memory lock feature to find the one that locked Mario in place. With that found, I just started inputting addresses nearby to find the X and Y coordinates.

Then, knowing I could get a readout of those, I stood at both ends of the bridge (at the corner, for additional accuracy) and measured my coordinates. From this I can use the Distance Formula [d = sqrt((x2 - x1)2 + (y2 - y1)2)] to figure out the length of the bridge.

The teeter totter bridge is 1815.23 (or so) units long, which is 19.54 meters. Knowing that it has to be 1 meter tall, we can use some trigonometry to figure out what angle the ramp has to be at.

sin(opp/hyp) = sin(1 / 19.54) = 2.93°. That's a nice, shallow angle. Why is this important? The angle we have changes the force we need to apply to King Bob-omb to pull him up the ramp, because now we're fighting against gravity. With a shallower angle, we don't have to fight AS much. (We are, of course, ignoring the thickness of the bridge. In reality, you might need to bury half of it underground or something to create a smooth transition from the dirt to the bridge.)

Namely, our force doesn't need to exceed µFn anymore. Now Ff ≥ Fg * sin(θ) + µFg * cos(θ), where Fg is the force due to gravity (what we once called our normal force when they were the same) and θ is our slope's angle. (I'm skipping a few steps with the physics here. Hit up an introductory physics course if you need help on deriving that.) Plugging everything in (using 0.25 for the coefficient of friction as stated earlier), and we need to pull with 154,200 newtons of force. This is less than the force required to make him move, so we need actually need a minimum of 302,474 newtons of force.

Enough dancing around the question now. How many people do we need to lift AND DEFEAT King Bob-omb? The answer: 237 people. Assuming that you're starting from the dirt, not the wood, and that everybody can sustain pulling at 1285 N of force for however long that would take.

The mighty ruler of the once great land, reduced to a mere bowling ball in power, tumbles a slow and eventful fall off his ramp. The brave heroes, tired after pouring their hearts out and into that act of pulling, gaze at the serenity of the sunset. It's a positively beautiful thing to reward them for their hard work. Mighty Mr. Bob-omb thuds into the ground at a staggering velocity. The ground resonates from the sheer force of his impact with the ground. The band of brothers and sisters turn back and look at their advesary, hopelessly lodged into the ground. It's done. He's defeated. ...Hah! You wish. They still have to dig him out and do that 2 more times for that pesky little star. You work isn't done yet, but my physics lesson is.

For the heck of it, here's a Javascript calculator that goes and re-computes the entire scenario, so you can play with numbers all you wish.